
La fisica per strada
Scoprire la fisica in automobile e in motocicletta

Come è possibile mettere in relazione lo spazio percorso con il tempo impiegato?
Abbiamo detto che nella descrizione del moto degli oggetti, oltre allo spazio percorso, è utile tenere in considerazione un’altra caratteristica misurabile in maniera oggettiva: il tempo impiegato per percorrerlo. Queste due grandezze possono essere messe in relazione per stabilire con che rapidità avvengono gli spostamenti e quindi per definire la velocità con cui si muove un veicolo.
Si definisce velocità media il rapporto tra lo spostamento del corpo e l’intervallo di tempo in cui esso è avvenuto. In particolare se t1, t2 sono rispettivamente i tempi in cui l'oggetto si trova nella posizione s1 e s2, allora
Essa è quindi diretttamente proporzionale alla distanza percorsa e inversamente proporzionale all'intervallo di tempo impiegato. Con questa definizione la velocità media è una grandezza scalare. Se invece si considera il vettore spostamento che congiunge il punto iniziale con quello finale, dotato quindi di una certa direzione e un certo verso, si definisce la velocità media come una grandezza vettoriale:
L’unità di misura della velocità è m/s (metri al secondo).

Le grandezze che descrivono il moto
Il nostro obiettivo è quello di analizzare alcuni fenomeni fisici che riguardano l'automobile e il suo moto, [... sicurezza stradale]. Il primo passo da compiere è descrivere il moto del veicolo: quali sono le grandezze di cui dobbiamo tenere conto per ottenere una rappresentazione più obiettiva e generale possibile?

Se si vuole descrivere il moto di un veicolo lungo una strada in modo formale, bisogna individuare degli aspetti che siano misurabili e non soggettivi, ovvero valutabili nella stessa maniera da osservatori diversi. Inoltre è necessario capire quali sono i parametri che influiscono su ciò che vogliamo studiare, tralasciando in un primo approccio le caratteristiche meno importanti. Supponiamo ad esempio di voler studiare il moto di quest'automobile lungo un tratto di circuito. Sicuramente dovremmo tener conto della lunghezza del tratto e del tempo impiegato per percorrerlo, mentre altri aspetti, come il colore dell'automobile, il rumore o la luminosità dei fari possono essere trascurati.

Per descrivere con precisione il moto di un veicolo, bisognerebbe inoltre analizzare il moto di ogni sua singola componente. Tuttavia in questo modo il problema si complica notevolmente e bisognerebbe ricorrere ai sistemi di particelle e alla teoria dei corpi rigidi. Questo esula dagli obiettivi della presente unità didattica, perciò semplificheremo l’oggetto in movimento considerandolo come un punto materiale, ovvero come un unico corpo puntiforme. Stiamo quindi modellizzando il problema in astratto: tale scelta ci permetterà di non considerare il movimento di ogni sua singola parte ma di capire ugualmente cosa accade quando un’automobile o una moto viaggiano per strada. Fino a che punto questa approssimazione ha senso e non influisce in maniera significativa sull'analisi del moto? Formalmente diremo che un corpo può essere approssimato ad un punto materiale quando le sue dimensioni sono trascurabili rispetto alle distanze che percorre.
Le grandezze che consideriamo sono quindi:
-
lo spazio percorso,
-
il tempo impiegato per percorrere tale spazio.
Grandezze fondamentali:
Grandezze trascurabili:
-
colore del veicolo
-
marca
-
rumore
-
...
-
tempo impiegato
-
spazio percorso
Cosa si intende per spazio percorso?
Durante uno spostamento il punto materiale (che, ricordiamo, corrisponde al veicolo di cui vogliamo descrivere il moto in ogni istante) può occupare punti diversi dello spazio. In particolare chiameremo traiettoria l’insieme dei punti corrispondenti alla posizione di un punto materiale in moto, ovvero la linea descritta nello spazio da un punto in movimento.
Consideriamo per iniziare un moto unidimensionale, ovvero che può essere descritto mediante un'unica coordinata spaziale. Si pensi ad esempio a un camion che percorre una strada rettilinea. Supponiamo di sovrapporre la strada a una retta e di fissare un punto origine, che indicheremo con O, e un verso positivo. In questo modo possiamo conoscere la coordinata di ogni punto sulla strada e la chiameremo posizione del punto.
La misura dello spazio percorso dal camion corrisponde quindi alla distanza.
Più formalmente se all’inizio del moto il corpo si trova nella posizione s1 e alla fine si trova nella posizione s2 allora si dice spostamento l’intervallo spaziale tra tali coordinate e si indica con:
Lo spostamento è quindi una lunghezza e si misura in metri (m).
Tuttavia il moto rettilineo è un caso particolare, mentre sono molto più comuni moti qualsiasi, di oggetti che spaziano liberamente in tutte le direzioni.




Per descrivere la generica posizione del punto materiale nello spazio sono necessarie tre coordinate: P(x,y,z). Essa può essere indicata con un vettore, detto vettore posizione, che congiunge l’origine del sistema di riferimento con quel punto dello spazio. In cinematica si definisce spostamento il cambiamento di posizione di un punto materiale in movimento. Dati due vettori posizione dello stesso punto in istanti di tempo diversi, il vettore spostamento è dato dalla differenza dei due vettori e viene indicato con .

Un'altra unità di misura comunemente utilizzata per la velocità è il kilometro all'ora (km/h), con cui è espressa sul tachimetro la velocità delle nostre automobili. Vediamo come convertire le due unità di misura:
-
da km/h in m/s: si divide per 3.6
-
da m/s in km/h: si moltiplica per 3.6
Esempio - Durante la terza tappa del Giro D'Italia, il vincitore percorre gli ultimi 500 metri che lo separano dal traguardo in 30 secondi. Qual è la sua velocità media?




Tuttavia durante un viaggio in automobile o in moto la velocità del veicolo in un istante ben preciso può variare da quella media, basta pensare a cosa succede quando ci si trova di fronte ad un ostacolo oppure quando si affronta una curva. Vedremo più avanti cosa significa variare la velocità di un veicolo, concentriamoci per il momento sulla misura istantanea della velocità. Il tachimetro ha proprio il compito di misurare la velocità istantanea del mezzo su cui è montato.
La velocità istantanea di un punto materiale in movimento si può calcolare a partire dalla velocità media vettoriale rendendo molto piccolo l’intervallo di tempo. Nel gergo matematico si dice che si fa “tendere a zero” l’intervallo di tempo e si utilizza il concetto di limite in questa maniera:
Approfondimento: autovelox e tutor
La polizia stradale, per vigilare sul rispetto dei limiti di velocità, nelle autostrade rileva sia la velocità media che quella istantanea attraverso due strumenti: l’autovelox, che è in grado di rilevare la velocità istantanea del veicolo, e il tutor che, grazie a due rilevamenti successivi, solitamente a distanza di circa 15 km, calcola la velocità media del veicolo. In questo modo anche se un veicolo rallenta in prossimità delle due fotocellule, se la sua velocità è in media sopra a quella del limite consentito, verrà sanzionato per eccesso di velocità.

Esercizi su velocità
Alcuni tipi di moto
La legge oraria e il grafico spazio-tempo
La matematica viene incontro all’esigenza di determinare la posizione esatta di un oggetto in movimento con una funzione, detta legge oraria, che associa ad un istante di tempo il punto dello spazio in cui si trova il punto materiale analizzato. La legge oraria permette di conoscere la traiettoria che l’oggetto percorre nello spazio.
Questa funzione si può rappresentare in un grafico che ha sull'asse delle ascisse il tempo t e sulle ordinate la posizione s di un punto materiale in movimento. Tale grafico ci fornisce importanti informazioni sul tipo di moto che sta compiendo l'oggetto. Ad esempio:
Per ogni tipo di moto è possibile determinare una legge oraria, vediamo quindi quali tipi di moto si possono avere.
Il moto rettilineo uniforme
Il più semplice tipo di movimento è quello che un corpo compie lungo una retta e a velocità costante. In questo caso lo spostamento del punto materiale può essere rappresentato da un vettore caratterizzato da:
-
direzione coincidente con la retta lungo la quale avviene il moto;
-
verso che indica il senso del movimento del punto;
-
modulo pari alla distanza del punto finale da quello iniziale.
Assumiamo che il moto in analisi stia avvenendo lungo la retta dello spazio rappresentata dall’asse delle x. Consideriamo le due posizioni x1 e x2 che il punto materiale occupa in due istanti di tempo successivi t1 e t2. In base alle definizioni date precedentemente possiamo calcolare in questo modo la velocità media, che in questo caso è costante e coincide con quella istantanea:
Un corpo compie un moto rettilineo uniforme se percorre spazi uguali in tempi uguali con velocità data dal vettore di modulo vm. Se fissiamo come istante iniziale t0=0, la precedente formula della velocità media si riduce in
Quest’ultima è la legge oraria del moto rettilineo uniforme. Se il punto materiale inizia il moto all’istante t=0 da una posizione x0, si ha quindi che:
Il grafico spazio-tempo, nel caso del moto rettilineo uniforme, è una retta di pendenza v che interseca l’asse delle ordinate nel punto (0,x0).

Il grafico spazio-tempo mostra che per t=0 il corpo si trova in posizione s=2, mentre dopo 4 s è giunto in s=6. Non solo: esso ci suggerisce che la posizione varia linearmente con il tempo. Vedremo che questa è una caratteristica di un moto a velocità costante (detto anche uniforme) e che in generale la legge oraria ci dà informazioni anche sulla velocità e su come essa varia nel tempo.



Questo grafico rappresenta un motto rettilineo uniforme. Possiamo osservare che per t=0 il corpo si trova nella posizione s0 (posizione iniziale) e che lo spazio cresce in maniera lineare con il tempo. La pendenza della retta indica la velocità del corpo.




Approfondimento
spazio di frenata


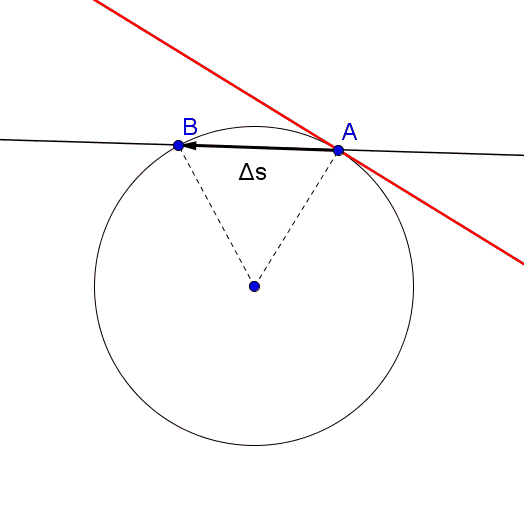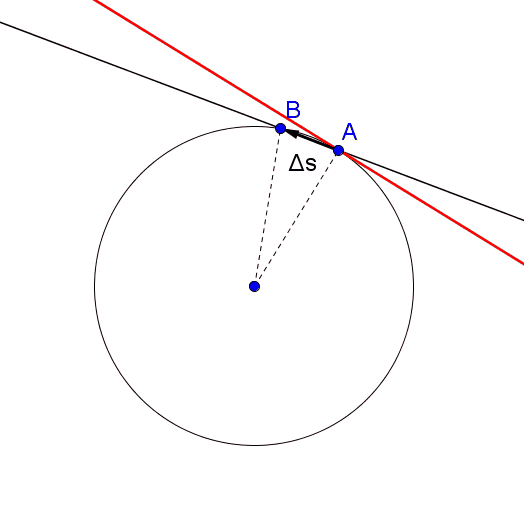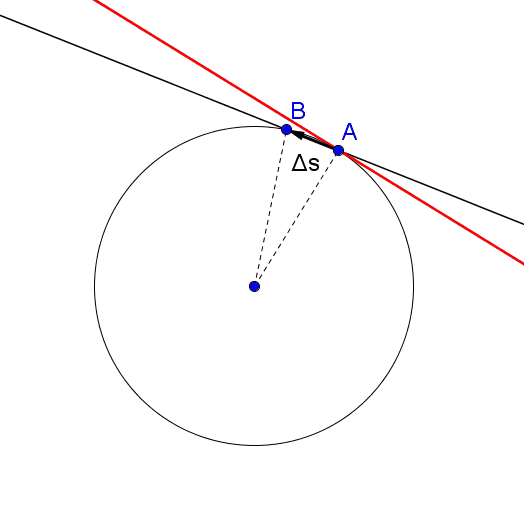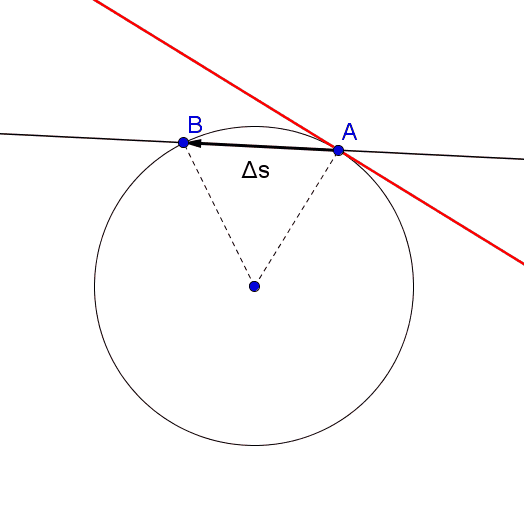
Mentre il corpo si muove da A a B sulla circonferenza, il raggio vettore spazza un angolo al centro AOB. La velocità angolare media è il vettore che ha come modulo il rapporto tra lo spostamento angolare del corpo e l’intervallo di tempo impiegato a compiere tale spostamento, la direzione perpendicolare al piano della circonferenza e verso dato dalla regola della mano destra.


L'accelerazione centripeta
Nel moto circolare uniforme il vettore velocità tangenziale, anche se costante in modulo, continua a cambiare direzione. Questa variazione è significativa del fatto che sul corpo in movimento sta agendo un’accelerazione. Si può dimostrare che tale accelerazione è pari a
ed è diretta verso il centro della circonferenza e perciò viene chiamata accelerazione centripeta. Il termine “centripeta” venne coniato da Newton, deriva dal latino e significa proprio “che tende al centro”.
Come si dimostra la formula dell'accelerazione centripeta?
Consideriamo il vettore velocità tangenziale: esso è sempre diretto lungo la tangente alla circonferenza ed è quindi perpendicolare al raggio vettore. Se si spostano graficamente i vettori velocità tangenziale in modo che la loro origine coincida, si vede che al variare del tempo la punta del vettore velocità descrive un moto circolare uniforme, in particolare essa descriverà un giro completo quando anche il raggio vettore spazzerà l’intera circonferenza. Di conseguenza i due vettori v e r hanno lo stesso periodo. Possiamo pensare che alla punta di v sia associato un “vettore velocità della velocità” che corrisponde proprio al vettore accelerazione centripeta. Il vettore ac è tangente alla traiettoria di v e quindi ne è perpendicolare (figura A). A sua volta v è perpendicolare a r e perciò i due vettori ac e r risultano paralleli e con versi opposti (figura B).

Qual è la velocità angolare delle lancette dei secondi, dei minuti e delle ore di un orologio?
Supponendo che le tre lancette siano lunghe rispettivamente 15 cm, 12.5 cm e 10 cm, qual è la velocità tangenziale della punta delle lancette?
Quanti kilometri percorre la punta della lancetta dei secondi nell'arco di un giorno?


Ad esempio, consideriamo una giostra che ruota con moto circolare uniforme di periodo T. Tutti i punti della giostra si muovono con la stessa velocità angolare, però i punti più vicini al centro della giostra sono più lenti di quelli che si trovano sul bordo. Ciò è espresso dalla formula appena espressa, quindi il modulo v della velocità dei punti della giostra aumenta in modo direttamente proporzionale alla loro distanza dal centro.

In conclusione il vettore accelerazione centripeta è diretto verso il centro della circonferenza e possiamo ricavare un’espressione per il modulo. La relazione che lega v a r matematicamente deve essere la stessa tra a e v , perciò si ha:

A questo punto siamo in grado di descrivere almeno in prima approssimazione come si comporta una macchina che affronta una curva circolare: sappiamo che se percorre tratti di curva uguali in tempi uguali allora la sua velocità sarà costante e possiamo calcolare la sua velocità angolare media conoscendo l’angolo al centro corrispondente al tratto di circonferenza percorso.
Tuttavia per capire a cosa è dovuta la modifica della traiettoria rettilinea in una traiettoria curva è necessario introdurre alcuni concetti di dinamica, in particolare le forze di attrito. Questo ci permetterà di approfondire meglio lo studio del moto e saremo in grado di rispondere a domande del tipo: cosa permette ad una macchina di mantenere una traiettoria curva lungo la strada? Cosa le garantisce di non sbandare e cosa succede invece quando una macchina sbanda? Quali sono le misure di sicurezza da adottare al fine di evitare situazioni di pericolo?


Esercizi
Esercizi sul moto circolare uniforme
Il moto rettilineo uniformemente accelerato
Cerchiamo ora di capire come possiamo descrivere la situazione in cui varia la velocità di un corpo in movimento. Potremmo procedere analogamente a quanto fatto nel caso uniforme, ovvero mettendo in relazione la variazione di velocità e l’intervallo temporaneo in cui si ha tale variazione.
Si definisce accelerazione media il rapporto tra la variazione di velocità e l’intervallo di tempo in cui essa avviene. Consideriamo la variazione tra l’istante iniziale (i) e quello finale (f) del moto:
Se l’accelerazione è positiva il veicolo aumenta la sua velocità, se invece è negativa la diminuisce.
Procedendo analogamente a quanto fatto per la velocità, possiamo definire l’accelerazione istantanea come il limite dell’accelerazione media quando l’intervallo di tempo tende a zero:
L’unità di misura dell’accelerazione è m/s (metri al secondo quadrato).
Se un punto materiale si muove con accelerazione costante, ovvero se la sua velocità varia di quantità uguali in tempi uguali, allora si dice che il suo moto è uniformemente accelerato. Dalla formula per l’accelerazione media ricaviamo la formula inversa
da cui imponendo ti=0
Ricaviamo la formula per lo spostamento da quella del moto rettilineo uniforme, considerando come velocità media la media aritmetica delle due velocità date, ovvero:
Sostituendo al posto di vf la formula della velocità ricavata prima si ottiene:
In conclusione la legge oraria del moto uniformemente accelerato è data da:
Lavorando opportunamente con le formule viste finora è possibile ricavare una grandezza in funzione delle altre due e quindi riscrivere in diverse maniere questa legge oraria.
Supponiamo ad esempio di voler determinare lo spazio percorso conoscendo la velocità e l’accelerazione ma non il tempo. Vogliamo quindi fare in modo che nella legge oraria non compaia la variabile t. Possiamo ricavare dalla formula della velocità il tempo e usare come velocità la media aritmetica delle velocità date. Sostituiamo queste relazioni nella legge oraria e troviamo:
2
Approfondimento grafici velocità - tempo
Il moto circolare uniforme
Il moto circolare è il moto che realizza un punto materiale quando si muove lungo una circonferenza. Può capitare che anche i veicoli percorrano tratti di strada pressoché assimilabili ad archi di circonferenza, quindi ci occuperemo di analizzare anche questo tipo di moto.
Il vettore posizione di un punto materiale su una circonferenza è individuato dal raggio vettore che congiunge il centro della circonferenza con il punto. Il vettore spostamento è dato, come nel moto rettilineo, dalla differenza dei due vettori che individuano le due posizioni successive. Si capisce quindi che i vettori spostamento nel moto circolare continuano a cambiare in direzione e lo stesso succederà quindi anche al vettore velocità media, essendo dato dal rapporto dello spostamento sull’intervallo di tempo.
Nonostante la direzione del vettore velocità media vari continuamente, nel moto circolare uniforme esso si mantiene costante in modulo, infatti un punto che si muove di moto circolare uniforme percorre archi di circonferenza uguali in tempi uguali. Una caratteristica importante del moto circolare uniforme è che il vettore velocità istantanea è tangente alla circonferenza, infatti considerando intervalli di tempo sempre più piccoli, si ottengono spostamenti via via più piccoli e continuando a ridurre tali intervalli si ottiene che in un dato punto, ovvero in un dato istante, la direzione del vettore spostamento è uguale alla direzione della retta tangente alla circonferenza in quel punto.
In conclusione il vettore velocità istantanea ha modulo costante ma continua a cambiare direzione, che coincide con quella dello spostamento, rimanendo così tangente alla traiettoria. Osserviamo che tale vettore è perpendicolare al vettore raggio che individua la posizione del punto.
La velocità tangenziale
Come abbiamo detto nel moto circolare uniforme la velocità è costante, infatti un punto materiale percorre archi di circonferenza uguali in tempi uguali.
Possiamo definire il periodo (T) come l’intervallo di tempo impiegato dal corpo per compiere un giro completo e la frequenza (f) come il numero di giri compiuti nell’unità di tempo T, ovvero f=1/T. L’unità di misura del periodo è il secondo (s), mentre della frequenza è l'hertz (Hz).
La velocità tangenziale è la velocità di un corpo che si muove di moto circolare uniforme lungo una circonferenza di raggio r e che impiega un tempo T per percorrere l’intera circonferenza. Il suo modulo è costante ed è dato dalla relazione
mentre la sua direzione, in ogni punto, è quella della retta tangente alla circonferenza in quel punto. Dalla formula si osserva che la velocità è direttamente proporzionale al raggio ed è inversamente proporzionale al periodo.
La velocità angolare
La velocità angolare, detta anche velocità radiale, esprime la rapidità con cui il raggio spazza l’angolo al centro corrispondente all’arco di circonferenza percorso dal corpo.
L’unità di misura della velocità angolare è Rad/s (radianti al secondo). Essendo il radiante un numero puro, si ha che la velocità angolare ha le stesse dimensioni dell’inverso del tempo.
Dalla definizione di moto circolare uniforme si ha che il raggio vettore spazza angoli al centro uguali in intervalli di tempo uguali, questo significa che in un moto circolare uniforme con periodo T un punto materiale percorre un quarto di circonferenza in un tempo pari a T/4 , mezza circonferenza in T/2 e così via, pertanto il modulo della velocità angolare è costante e pari a
Da tale formula si osserva che la velocità angolare, a differenza della velocità tangenziale, non dipende dal raggio della circonferenza. Di conseguenza corpi che hanno la stessa velocità angolare, e quindi che descrivono angoli al centro uguali in intervalli di tempo uguali, possono avere velocità tangenziale diversa a seconda della loro distanza dal centro della circonferenza e possono quindi percorrere archi di circonferenza diversi. In formule si ha:




